1:2の三角形

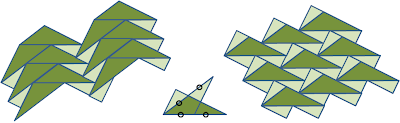
検討を進めると、二つの基本パターンが可能な3角形の組には、３０°の直角3角形だけではなく、二辺の比が１：２の3角形も含まれることが分かった。下中央の図を見れば、理解しやすい。色の濃い大きな3角形について、どちらのパターンでも、1:1と1:2に内分される辺と内分されない辺になっている。色が薄い小さな3角形は、左のパターンでは内分なし、右のパターンでは一辺が1:1に内分される3角形が二つ、残りの一つは内分なし。

# 大きな三角形の１：２の２辺の長さを変えずに、角度を変え、内分の関係を崩さずに変形させる動画を見ていたい。

上のような二つの基本パターンを作れる3角形は、今のところ、以下の三種が見つかっている。

直角二等辺3角形

二つの辺が１：２の3角形

辺が３：４：５の直角3角形

新パターンの検討

二つの基本パターンに使える3-4-5のc直角三角形

 新パターンの方を拡張。もう一つの基本パターンにはこの三角形の組は使えない。

30-60-90では？

基本パターンと新基本パターンを混在できる三角形の検討。

見落としていた三角形があった。長さの比が１：√３の30°の直角三角形のペアである。

両パターンが作れ、親和性も良さそうなのだが、まだ繋げる方法が見つからない。

基本パターンBの拡張

＃先の投稿に間違いが何箇所かあったので、修正。

基本パターンAと同様の拡張をパターンBでしてみた。
二等辺三角形の二分割による拡張は、パターンBでも同様にできる。パターンBでは、大きな3角形の辺の中点に小さな三角形の頂点が一般にこないので、大きな3角形も二等辺三角形であれば、二分割が可能である。ただし、正三角形は使えないので、ランダム二分割はできない。
二辺の比が１：２の三角形の二分割は、パターンBでは、余弦が約0.839287（Wolfram Alphaで算出）の直角3角形一種類のみである。

パターンAとパターンBとの混合パターンの直角二等辺3角形以外の可能性の考察。
大きな三角形と小さな三角形が相似となるのは、直角3角形の場合のみ。パターンBで、辺の中点に頂点が来るのは、30度の直角三角形の場合だが、長さが１：２ではないのでだめ。長さが１：２となるのは、3-4-5の直角三角形だが、辺の中点に頂点がこないのでだめ。
直角二等辺3角形の特殊性（自己相似の二倍体(？)の存在がキーか？）を再認識させられた。

#追加コメント
二辺の比が１：２の三角形の記述は間違い。どれでも可能でした。
どのように考えて、上記の0.839287の三角形が出てきたんだろう？自分でも分からない。

基本パターンB

新たな基本パターンが一般の三角形で作成可能であることの簡単な証明法を見つけた。下図の破線の三角形を追加すると、中学レベルで証明できる。

大きい方の三角形は、従来の基本パターン(Aとする）では、それを顔に見立てると、三方向に小さい三角形の耳を二つ持つ。新基本パターン（Bとする）では、二方向に二つの耳を持ち、残りの一辺は大きめの帽子（大きい三角）をかぶっている。基本パターンAは、大小の三角形は相似なので、失格パターン（基本パターンBと等価）に関するMINEさんの考察から、基本パターンAとBの混合は、直角二等辺三角形に限られることになる。

＃MINEさんのブログにある「３辺の比が １：２：ｘ （１＜ｘ＜３） である三角形すべてに適用できるパターン」も相似でない三角形で構成され、角度の構成もこれと同じだが、残念ながら大きさが一致しないようだ。

新たな「無しかくタイル」

いわいさんの命名に則り、パズル名を短縮しました。
さて、直角二等辺三角形を用いて、他の接続方法を探索して得たのが下図のパターン。大きな三角形の向きを変えようとしたものの、赤い境界線の接続は使えるのだが、青い方は四角が生じるので使えない。

渦巻き状接続は無理っぽいが、気を取り直して、下図のように大きい方のパターンを接続してみた。うまく接続できた上に、基本パターンから外れた接続になっている、

上図の大小パターン一列ずつを接続してみると、大きな三角形も小さな三角形もすべて倍の△で現れた。そこで、全部二個一にしたのが下図。逆にどちらの三角形も二等分できるので、１：３＋２√２  １：２＋√２や１：１＋√２／２の比の直角二等辺三角形でもOK。

大きな三角形の一辺が他の三角形の頂点と接しておらず、凹七角形が基本ユニットである点が、基本パターンと異なる。大きな三角形の一辺を分割する三角形の一部を大きな三角形が代用しているという意味で、省エネタイプと言えるかもしれない。

失格パターンと同様に、正三角形以外なら成立すると思われる。余弦定理等を使って、証明できたつもりだが、自信なし。検証やもっと簡単な証明を請う。

失格パターンその後（２）

共に二等辺三角形となる残りの失格パターン。

非周期配置

四角形の現れない三角形二種による平面分割問題の解の一つ、直角二等辺三角形二種による非周期配置がなぜうまく成立したのかを簡単に考察してみた。

もともと、下図に示すような二種類の周期解が見つかったのだが、赤線で示すような境界線が二つの解で全く同じであり、かつ境界線の両側の三角形の配列が両者で等価であったことが、非周期配置に幸いしたと考えられる。

境界間の相対関係が、両者で異なるので、見つかった解の一部を再構成して、上下方向にも非周期性を持たせるのは、かなり難しそうである。

失格パターンその後

一つ前の記事に書いた黄金比のパターンであるが、MINEさんから直角三角形でもできると教えていただいた。検討して見たところ、下図に示すように、一般の三角形で成立することが分かった。

最初は△ABCを回転移動して△AEDとしていたため、AD//BCとなるには、△ABCは二等辺三角形でなければなかった。さらに、必要条件ではないのに、△CEFもEFを底辺とする二等辺三角形としてしまったために、黄金比が出てくることになった。しかし、元の三角形を反転して、△ABC≡△DEAとなるようにすると、自動的に条件を満足してくれる。どんな三角形でも成立しそうだが、少なくとも一辺の長さが他辺の長さと異ならないといけないので、正三角形は不可だ。

四角形の現れない三角形二種による平面分割

いわいさんのブログで出題された上記タイトルの問題ですが、私自身はさっぱり分からず、いわいさんやＭＩＮＥさんのブログを見て、なるほどと感心していました。眺めているうちに思いついたのが、長さの比が１：１＋√２の直角二等辺三角形のペアを用いたパターンで、それまで示されていたパターンと異なり、基本パターンの大きな三角形の辺の中点に小さな三角形の頂点がこないことが新しい。その旨、いわいさんのブログにコメントしたのですが、その時点では、小さな三角形を三つ使うパターンしか気付いていませんでした。後に、大きな三角形を三つ使うパターンもあることが分かりました。
さらに長周期パターンを探っていると、上記の直角二等辺三角形のペアを使うと、下図のように、一方向に非周期的なパターンを作れることに気がつきました。当初のペンローズのタイル張りのようなパターンが作れないかという目論見に半歩だけ近づいた感じです。

基本パターンは、平行四辺形から角を共有する小さな平行四辺形を除いた凹六角形を周期的に並べたものであることに着目して、考えたのが下のパターンです。計算すると黄金比が出てきて、感激したのですが、よく見ると凹四角形が現れていて、失格でした。三角形何種類使っても、基本パターン（＋2分割）以外はだめなのかもしれません。